932. The height of triangle

The area of triangle is S. The length of its base is a greater than its height. Find the height of triangle.

Input. Two integers: S (0 < S ≤ 100) and a (|a| ≤ 100).

Output. Print the height of triangle with two digits after the decimal point.

Sample input	Sample output
15 1	5.00

SOLUTION

geometry - elementary

Algorithm analysis

Let h be the height of triangle. Then its base is h + a. The area of the triangle is S = ½ h (h + a). The values of S and a are given, solve the quadratic equation for h:

h² + ha – 2S = 0,

discriminant D = a² + 4S,

the positive root is h =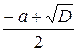

Algorithm realization

Read the input data. Solve the quadratic equation S = ½ h (h + a) for h and take its positive root.

scanf("%lf %lf",&s,&a);

d = a*a + 8*s;

h = (-a + sqrt(d)) / 2;

printf("%.2lf\n",h);

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

double s = con.nextDouble();

double a = con.nextDouble();

double d = a * a + 8 * s;

double h = (-a + Math.sqrt(d)) / 2;

System.out.println(h);

con.close();

}

}

Python realization

import math

s, a = map(float,input().split())

d = a*a + 8*s;

h = (-a + math.sqrt(d)) / 2;

print("%.2f" %h)